Gradient flows and the Łojasiewicz inequality, with an application to higher-order criticality
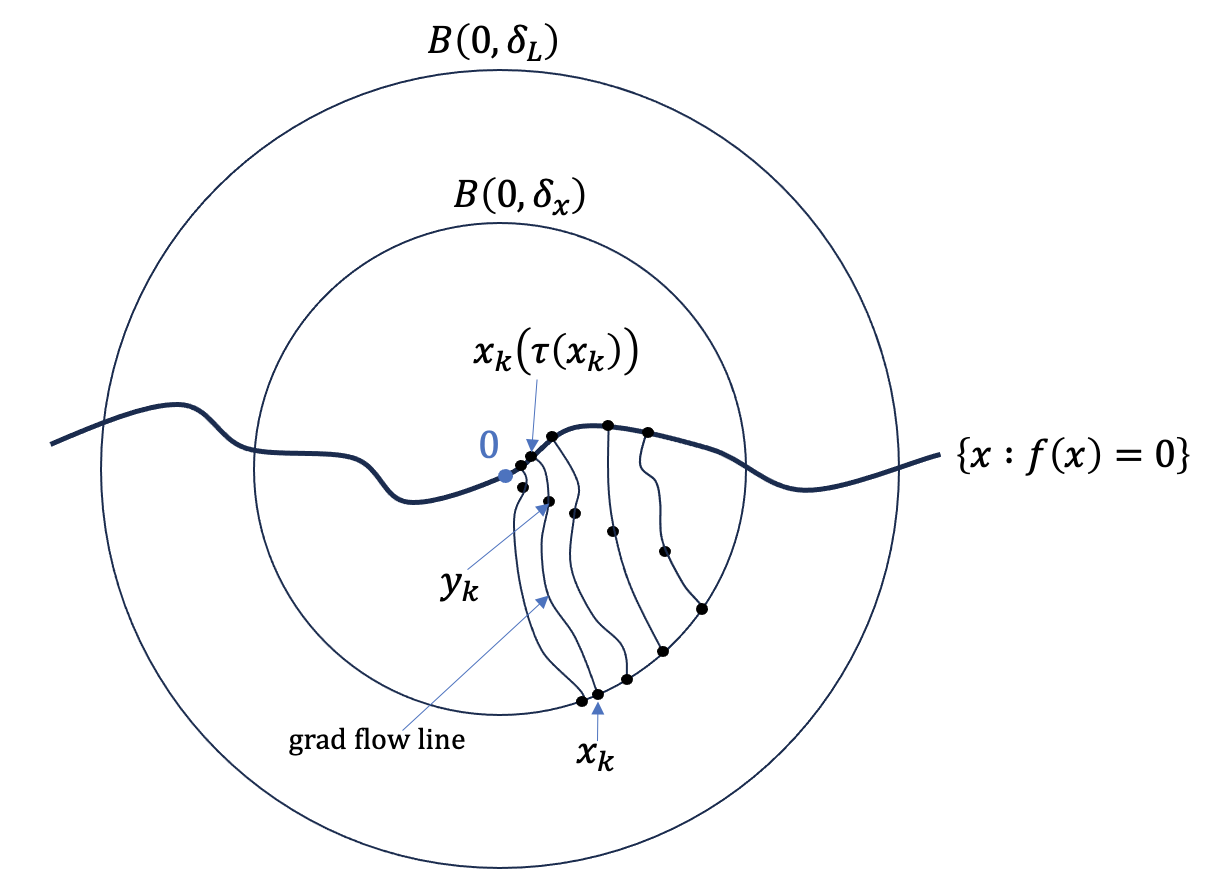
We show that every saddle point of a real-analytic function has a gradient flow line converging to it. We use this fact to prove a claim made in our previous blog post on higher-order criticality: if \(x\) is a \(p\)-critical point of a real-analytic function \(f\) for all positive integers \(p\), then \(x\) is a local minimum of \(f\). The key tools used throughout are gradient flows and the Łojasiewicz inequality.
Higher-order critical points: definitions and curiosities
Everyone knows what a 1st or 2nd order critical point is. But how do we define higher-order criticality? In this post we consider several natural definitions of higher-order critical points, and show that, surprisingly, these definitions are all different. Our goal is to point out some facts all optimizers should know (and which at times might be hard to find in a single place), and help avoid some common misconceptions.