Gradient flows and the Łojasiewicz inequality, with an application to higher-order criticality

We show that every saddle point of a real-analytic function has a gradient flow line converging to it. We use this fact to prove a claim made in our previous blog post on higher-order criticality: if \(x\) is a \(p\)-critical point of a real-analytic function \(f\) for all positive integers \(p\), then \(x\) is a local minimum of \(f\). The key tools used throughout are gradient flows and the Łojasiewicz inequality.

\[ \newcommand{\abs}[1]{\left|{#1}\right|} \newcommand{\argmax}[1]{\underset{#1}{\operatorname{argmax}}} \newcommand{\argmin}[1]{\underset{#1}{\operatorname{argmin}}} \newcommand{\bareta}{{\overline{\eta}}} \newcommand{\barf}{{\overline{f}}} \newcommand{\barg}{{\overline{g}}} \newcommand{\barM}{\overline{\mathcal{M}}} \newcommand{\barnabla}{\overline{\nabla}} \newcommand{\barRcurv}{\bar{\mathcal{R}}} \newcommand{\barRmop}{\bar{R}_\mathrm{m}} \newcommand{\barRmoptensor}{\mathbf{{\bar{R}_\mathrm{m}}}} \newcommand{\barx}{{\overline{x}}} \newcommand{\barX}{{\overline{X}}} \newcommand{\barxi}{{\overline{\xi}}} \newcommand{\bary}{{\overline{y}}} \newcommand{\barY}{{\overline{Y}}} \newcommand{\bfeta}{{\bm{\eta}}} \newcommand{\bfF}{\mathbf{F}} \newcommand{\bfOmega}{\boldsymbol{\Omega}} \newcommand{\bfR}{\mathbf{R}} \newcommand{\bftheta}{{\bm{\theta}}} \newcommand{\bfX}{{\mathbf{X}}} \newcommand{\bfxi}{{\bm{\xi}}} \newcommand{\bfY}{{\mathbf{Y}}} \newcommand{\calA}{\mathcal{A}} \newcommand{\calB}{\mathcal{B}} \newcommand{\calP}{\mathcal{P}} \newcommand{\calC}{\mathcal{C}} \newcommand{\calE}{\mathcal{E}} \newcommand{\calF}{\mathcal{F}} \newcommand{\calG}{\mathcal{G}} \newcommand{\calH}{\mathcal{H}} \newcommand{\calJ}{\mathcal{J}} \newcommand{\calK}{\mathcal{K}} \newcommand{\calL}{\mathcal{L}} \newcommand{\ones}{\textbf{1}} \newcommand{\calM}{\mathcal{M}} \newcommand{\calN}{\mathcal{N}} \newcommand{\calO}{\mathcal{O}} \newcommand{\calS}{\mathcal{S}} \newcommand{\calT}{\mathcal{T}} \newcommand{\calU}{\mathcal{U}} \newcommand{\calV}{\mathcal{V}} \newcommand{\calW}{\mathcal{W}} \newcommand{\calX}{\mathcal{X}} \newcommand{\Cm}{{\mathbb{C}^m}} \newcommand{\CN}{{\mathbb{C}^{\,N}}} \newcommand{\Cn}{\mathbb{C}^n} \newcommand{\CNN}{{\mathbb{C}^{\ N\times N}}} \newcommand{\Cnn}{\mathbb{C}^{n\times n}} \newcommand{\CnotR}{{\mathbb{C}\ \backslash\mathbb{R}}} \newcommand{\col}{\operatorname{col}} \newcommand{\im}{\operatorname{im}} \newcommand{\complex}{{\mathbb{C}}} \newcommand{\Cov}{\mathbf{C}} \newcommand{\Covm}{C} \newcommand{\Ric}{\mathrm{Ric}} \newcommand{\Rmcurv}{\mathrm{Rm}} \newcommand{\D}{\mathrm{D}} \newcommand{\dblquote}[1]{``#1''} \newcommand{\dd}[1]{\frac{\mathrm{d}}{\mathrm{d}#1}} \newcommand{\ddiag}{\mathrm{ddiag}} \newcommand{\ddp}[2]{\frac{\partial #1}{\partial #2}} \newcommand{\Ddq}{\frac{\D}{\dq}} \newcommand{\dds}{\frac{\mathrm{d}}{\mathrm{d}s}} \newcommand{\Ddt}{\frac{\D}{\dt}} \newcommand{\ddt}{\frac{\mathrm{d}}{\mathrm{d}t}} \newcommand{\Ddttwo}{\frac{\D^2}{\dt^2}} \newcommand{\defeq}{\triangleq} \newcommand{\Dexp}{\D\!\exp} \newcommand{\error}{\mathrm{error}} \newcommand{\diag}{\mathrm{diag}} \newcommand{\Diag}{\mathrm{Diag}} \newcommand{\Vol}{\mathrm{Vol}} \newcommand{\polylog}{\mathrm{polylog}} \newcommand{\poly}{\mathrm{poly}} \newcommand{\dist}{\mathrm{dist}} \newcommand{\Dlog}{\D\!\log} \newcommand{\dmu}{\mathrm{d}\mu} \newcommand{\dphi}{\mathrm{d}\phi} \newcommand{\dq}{\mathrm{d}q} \newcommand{\ds}{\mathrm{d}s} \newcommand{\dt}{\mathrm{d}t} \newcommand{\dtau}{\mathrm{d}\tau} \newcommand{\dtheta}{\mathrm{d}\theta} \newcommand{\du}{\mathrm{d}u} \newcommand{\dx}{\mathrm{d}x} \newcommand{\Ebad}{E_\textrm{bad}} \newcommand{\Egood}{E_\textrm{good}} \newcommand{\eig}{{\mathrm{eig}}} \newcommand{\ellth}{$\ell$th } \newcommand{\embdist}{\mathrm{embdist}} \newcommand{\ER}{{Erd\H{o}s-R\'enyi }} \newcommand{\Exp}{\mathrm{Exp}} \newcommand{\expect}{\mathbb{E}} \newcommand{\expectt}[1]{\mathbb{E}\left\{{#1}\right\}} \newcommand{\expp}[1]{{\exp\!\big({#1}\big)}} \newcommand{\feq}{{f_\mathrm{eq}}} \newcommand{\FIM}{\mathbf{F}} \newcommand{\FIMm}{F} \newcommand{\floor}[1]{\lfloor #1 \rfloor} \newcommand{\flow}{f_{\mathrm{low}}} \newcommand{\FM}{\mathfrak{F}(\M)} \newcommand{\frobnorm}[2][F]{\left\|{#2}\right\|_\mathrm{#1}} \newcommand{\frobnormbig}[1]{\big\|{#1}\big\|_\mathrm{F}} \newcommand{\frobnormsmall}[1]{\|{#1}\|_\mathrm{F}} \newcommand{\GLr}{{\mathbb{R}^{r\times r}_*}} \newcommand{\Gr}{\mathrm{Gr}} \newcommand{\grad}{\mathrm{grad}} \newcommand{\Hess}{\mathrm{Hess}} \newcommand{\HH}{\mathrm{H}} \newcommand{\Id}{\operatorname{Id}} % need to be distinguishable from identity matrix \newcommand{\II}{I\!I} \newcommand{\inj}{\mathrm{inj}} \newcommand{\inner}[2]{\left\langle{#1},{#2}\right\rangle} \newcommand{\innerbig}[2]{\big\langle{#1},{#2}\big\rangle} \newcommand{\innersmall}[2]{\langle{#1},{#2}\rangle} \newcommand{\ith}{$i$th } \newcommand{\jth}{$j$th } \newcommand{\Klow}{{K_{\mathrm{low}}}} \newcommand{\Kmax}{K_{\mathrm{max}}} \newcommand{\kth}{$k$th } \newcommand{\Kup}{{K_{\mathrm{up}}}} \newcommand{\Klo}{{K_{\mathrm{lo}}}} \newcommand{\lambdamax}{\lambda_\mathrm{max}} \newcommand{\lambdamin}{\lambda_\mathrm{min}} \newcommand{\langevin}{\mathrm{Lang}} \newcommand{\langout}{\mathrm{LangUni}} \newcommand{\length}{\operatorname{length}} \newcommand{\Log}{\mathrm{Log}} \newcommand{\longg}{{\mathrm{long}}} \newcommand{\M}{\mathcal{M}} \newcommand{\mle}{{\mathrm{MLE}}} \newcommand{\mlez}{{\mathrm{MLE0}}} \newcommand{\MSE}{\mathrm{MSE}} \newcommand{\N}{\mathrm{N}} \newcommand{\norm}[1]{\left\|{#1}\right\|} \newcommand{\nulll}{\operatorname{null}} \newcommand{\hull}{\mathrm{hull}} \newcommand{\Od}{{\mathrm{O}(d)}} \newcommand{\On}{{\mathrm{O}(n)}} \newcommand{\One}{\mathds{1}} \newcommand{\Op}{{\mathrm{O}(p)}} \newcommand{\opnormsmall}[1]{\|{#1}\|_\mathrm{op}} \newcommand{\p}{\mathcal{P}} \newcommand{\pa}[1]{\left(#1\right)} \newcommand{\paa}[1]{\left\{#1\right\}} \newcommand{\pac}[1]{\left[#1\right]} \newcommand{\pdd}[1]{\frac{\partial}{\partial #1}} \newcommand{\polar}{\mathrm{polar}} \newcommand{\Precon}{\mathrm{Precon}} \newcommand{\proj}{\mathrm{proj}} \newcommand{\Proj}{\mathrm{Proj}} \newcommand{\ProjH}{\mathrm{Proj}^h} \newcommand{\PSD}{\mathrm{PSD}} \newcommand{\ProjV}{\mathrm{Proj}^v} \newcommand{\qf}{\mathrm{qf}} \newcommand{\rank}{\operatorname{rank}} \newcommand{\Rball}{R_{\mathrm{ball}}} \newcommand{\Rcurv}{\mathcal{R}} \newcommand{\Rd}{{\mathbb{R}^{d}}} \newcommand{\Rdd}{{\mathbb{R}^{d\times d}}} \newcommand{\Rdp}{{\mathbb{R}^{d\times p}}} \newcommand{\reals}{{\mathbb{R}}} \newcommand{\Retr}{\mathrm{R}} \newcommand{\Rk}{{\mathbb{R}^{k}}} \newcommand{\Rm}{{\mathbb{R}^m}} \newcommand{\Rmle}{{\hat\bfR_\mle}} \newcommand{\Rmm}{{\mathbb{R}^{m\times m}}} \newcommand{\Rmn}{{\mathbb{R}^{m\times n}}} \newcommand{\Rmnr}{{\mathbb{R}_r^{m\times n}}} \newcommand{\Rmop}{R_\mathrm{m}} \newcommand{\Rmoptensor}{\mathbf{{R_\mathrm{m}}}} \newcommand{\Rmr}{\mathbb{R}^{m\times r}} \newcommand{\RMSE}{\mathrm{RMSE}} \newcommand{\Rn}{{\mathbb{R}^n}} \newcommand{\Rnk}{\mathbb{R}^{n\times k}} \newcommand{\Rnm}{\mathbb{R}^{n\times m}} \newcommand{\Rnn}{{\mathbb{R}^{n\times n}}} \newcommand{\RNN}{{\mathbb{R}^{N\times N}}} \newcommand{\Rnp}{{\mathbb{R}^{n\times p}}} \newcommand{\Rnr}{\mathbb{R}^{n\times r}} \newcommand{\Rp}{{\mathbb{R}^{p}}} \newcommand{\Rpp}{\mathbb{R}^{p\times p}} \newcommand{\Rrn}{{\mathbb{R}^{r\times n}}} \newcommand{\Rrr}{\mathbb{R}^{r\times r}} \newcommand{\Rtt}{{\mathbb{R}^{3\times 3}}} \newcommand{\sbd}[1]{\sbdop\!\left({#1}\right)} \newcommand{\sbdop}{\operatorname{symblockdiag}} \newcommand{\sbdsmall}[1]{\sbdop({#1})} \newcommand{\Sd}{\mathbb{S}^{d}} \newcommand{\Sdd}{{\mathbb{S}^{d\times d}}} \newcommand{\short}{{\mathrm{short}}} \newcommand{\sigmamax}{\sigma_{\operatorname{max}}} \newcommand{\sigmamin}{\sigma_{\operatorname{min}}} \newcommand{\sign}{\mathrm{sign}} \newcommand{\ske}{\operatorname{skew}} \newcommand{\Skew}{\operatorname{Skew}} \newcommand{\skeww}[1]{\operatorname{skew}\!\left( #1 \right)} \newcommand{\Sm}{\mathbb{S}^{m-1}} \newcommand{\smallfrobnorm}[1]{\|{#1}\|_\mathrm{F}} \newcommand{\Smdmd}{{\mathbb{S}^{md\times md}}} \newcommand{\Smm}{{\mathbb{S}^{m\times m}}} \newcommand{\Sn}{\mathbb{S}^{n-1}} \newcommand{\Snn}{{\mathbb{S}^{n\times n}}} \newcommand{\So}{{\mathbb{S}^{1}}} \newcommand{\SOd}{\operatorname{SO}(d)} \newcommand{\SOdm}{\operatorname{SO}(d)^m} \newcommand{\son}{{\mathfrak{so}(n)}} \newcommand{\SOn}{{\mathrm{SO}(n)}} \newcommand{\sot}{{\mathfrak{so}(3)}} \newcommand{\SOt}{{\mathrm{SO}(3)}} \newcommand{\sotwo}{{\mathfrak{so}(2)}} \newcommand{\SOtwo}{{\mathrm{SO}(2)}} \newcommand{\Sp}{{\mathbb{S}^{2}}} \newcommand{\spann}{\mathrm{span}} \newcommand{\gspan}{\mathrm{gspan}} \newcommand{\Spp}{{\mathbb{S}^{p\times p}}} \newcommand{\sqfrobnorm}[2][F]{\frobnorm[#1]{#2}^2} \newcommand{\sqfrobnormbig}[1]{\frobnormbig{#1}^2} \newcommand{\sqfrobnormsmall}[1]{\frobnormsmall{#1}^2} \newcommand{\sqnorm}[1]{\left\|{#1}\right\|^2} \newcommand{\Srr}{{\mathbb{S}^{r\times r}}} \newcommand{\St}{\mathrm{St}} \newcommand{\Cent}{\mathrm{Centered}} \newcommand{\Holl}{\mathrm{Hollow}} \newcommand{\Stdpm}{\St(d, p)^m} \newcommand{\Stnp}{{\mathrm{St}(n,p)}} \newcommand{\Stwo}{{\mathbb{S}^{2}}} \newcommand{\symm}[1]{\symmop\!\left( #1 \right)} \newcommand{\symmop}{\operatorname{sym}} \newcommand{\symmsmall}[1]{\symmop( #1 )} \newcommand{\Symn}{\mathrm{Sym}(n)} \newcommand{\Symnminp}{\mathrm{Sym}(n-p)} \newcommand{\Symp}{\mathrm{Sym}(p)} \newcommand{\Sym}{\mathrm{Sym}} \newcommand{\T}{\mathrm{T}} \newcommand{\TODO}[1]{{\color{red}{[#1]}}} \newcommand{\trace}{\mathrm{Tr}} \newcommand{\Trace}{\mathrm{Tr}} \newcommand{\Trans}{\mathrm{Transport}} \newcommand{\Transbis}[2]{\mathrm{Transport}_{{#1}}({#2})} \newcommand{\transpose}{^\top\! } \newcommand{\uniform}{\mathrm{Uni}} \newcommand{\var}{\mathrm{var}} \newcommand{\vecc}{\mathrm{vec}} \newcommand{\veccc}[1]{\vecc\left({#1}\right)} \newcommand{\VV}{\mathrm{V}} \newcommand{\XM}{\mathfrak{X}(\M)} \newcommand{\xorigin}{x_{\mathrm{ref}}} \newcommand{\Zeq}{{Z_\mathrm{eq}}} \newcommand{\aref}[1]{\hyperref[#1]{A\ref{#1}}} \newcommand{\frobnorm}[1]{\left\|{#1}\right\|_\mathrm{F}} \newcommand{\sqfrobnorm}[1]{\frobnorm{#1}^2} \]

Introduction

In our previous blog post, we considered several definitions of \(p\)-criticality (through straight lines, curves and neighborhoods), and showed none of these definitions are equivalent. Let’s recall them here:

Definitions of \(p\)-critical point

The point \(x \in \reals^d\) is \(p\)-critical for \(f\) through “straight lines”, “curves”, or “neighborhoods” if:

1. [through straight lines] For all \(v \in \mathbb{R}^d\), the 1D function \(t \mapsto f(x + t v)\) has a \(p\)-th order critical point at \(t=0\).

2. [through curves] For all \(C^p\) curves \(\gamma\) with \(\gamma(0) = x\) and \(\gamma'(0) \neq 0\), the 1D function \(t \mapsto f(\gamma(t))\) has a \(p\)-th order critical point at \(t=0\).

3. [through neighborhoods] There is an \(\epsilon > 0\) and \(C > 0\) such that \(f(x + v) \geq f(x) - C \|v\|^{p+1}\) for all \(v \in \reals^d\) such that \(\|v\| \leq \epsilon\). (This is definition 1 in this paper of Anandkumar and Ge.)

We concluded that the “right” definition of \(p\)-criticality is through neighborhoods, due to the following two properties (not enjoyed by the other definitions).

Proposition 1

If \(f \colon \reals^d \to \reals\) is real-analytic and \(0\) is \(p\)-critical through neighborhoods for all \(p \geq 1\), then \(0\) is a local minimum of \(f\).

Proposition 2

For each \(d \geq 1\) and \(k \geq 1\), there is a (finite) positive integer \(p(k,d)\) such that: if \(f \colon \reals^d \to \reals\) is a degree-\(k\) polynomial and \(0\) is \(p(k,d)\)-critical through neighborhoods, then \(0\) is a local minimum of \(f\).

Counterexamples: Propositions 1 and 2

For Proposition 1, the real-analytic assumption is necessary, i.e., \(f\) being \(C^\infty\) is not enough — recall the 1D counterexample \(f(x) = x e^{-1/x^2}\) from our previous blog post.

For Proposition 2, it is easy to show that \(p(k, 1) = k\) works. However, for \(d > 1\), \(p(k, d) = k\) is not enough — recall the counterexample \[f(x,y) = y^2 - x^2 y - x y^2\] from our previous blog post. We argued that \((0,0)\) is \(3\)-critical for \(f\), but it is not a local minimum (hence \(p(3, 2) > 3\)). Exercise: Show that \(p(3, 2) = 5\) works.

Propositions 1 and 2 are consequences of the following result.

Proposition 3

Let \(f \colon \reals^d \to \reals\) be real-analytic, with \(f(0) = 0, \nabla f(0) = 0\). If \(0\) is not a local minimum of \(f\), then there exists \(x_0 \in \reals^d \setminus \{0\}\) such that positive gradient flow \(\eqref{posgradflow}\) started from \(x_0\) converges to \(0\).

Proposition 3 is probably known — see these papers of Moussu, Nowel and Szafraniec, and Szafraniec. We present a proof at the end of this post. This proof may be new, and, more importantly, it is self-contained and hopefully easy to parse!

The key tools to prove Propositions 1, 2, 3 are gradient flows and the Łojasiewicz inequality.

Counterexample: Proposition 3

The assumption that \(f\) is real-analytic in Propostion 3 is necessary, i.e., it is not enough for \(f\) to be only \(C^\infty\). Indeed, consider a smooth 1D function which oscillates infinitely often, like the following: \[f(x) = \sin(6\pi/x) e^{-1/x^2}.\] Non-constant gradient flow trajectories cannot converge to the origin because there are \(1\)-critical points arbitrarily close to it (on both sides).

The function above is somewhat pathological as its set of \(1\)-critical points is not a smooth manifold. What if we additionally assume the set of \(1\)-critical points of \(f\) is a smooth manifold? Even this is not enough for Proposition 3 to hold: an example is furnished by the so-called “Mexican hat function” and variants thereof (see pages 4-5 in this paper by Absil, Mahony and Andrews).

Figure 1: Plot of \(f(x) = \sin(6\pi/x) e^{-1/x^2}\).

Gradient flows

Let \(f \colon \reals^d \to \reals\) be \(C^\infty\). A positive gradient flow trajectory started at \(x_0 \in \reals^d\) is a solution of the ODE \[ \begin{align}\label{posgradflow}\tag{$+\text{gradflow}$} x'(t) = \nabla f(x(t)), \quad \quad t \in \reals, \quad \quad x(0) = x_0. \end{align} \] Likewise, negative gradient flow is a solution of \[ \begin{align}\label{neggradflow}\tag{$-\text{gradflow}$} x'(t) = -\nabla f(x(t)), \quad \quad t \in \reals, \quad \quad x(0) = x_0. \end{align} \] A gradient flow is always defined on some open interval around \(t = 0\); however, it may not be defined on all of \(\reals\). If \(\nabla f(x_0)\) is nonzero then gradient flow never reaches a \(1\)-critical point in finite time (since the flow map \(\Phi\) defined below is a diffeomorphism in an appropriate sense). Therefore, the quantity \(f(x(t))\) is always increasing for positive gradient flow with \(\nabla f(x_0) \neq 0\). This is because \[\frac{d}{dt}[f(x(t))] = \D f(x(t))[x'(t)] = \|\nabla f(x(t))\|^2 > 0 \quad \quad \text{for all $t$}.\] (And likewise the function value decreases for negative gradient flow.)

We define the positive gradient flow map \(\Phi\) by \[ \begin{align}\label{flowmap}\tag{flowmap} \Phi(x_0, t) = x(t) \end{align} \] where \(x(\cdot)\) is the positive gradient flow starting at \(x_0\). The flow map \(\Phi\) is defined on a (open) subset of \(\reals^d \times \reals\) (this domain is called the flow’s maximal flow domain). It is a fact that \(\Phi\) is differentiable on its domain. Further, for a given \(t\), the map \(x \mapsto \Phi(x, t)\) is a diffeomorphism (from the set of points on which it is well defined and onto its image). For more information on vector-field flows more generally, we recommend Chapter 9 “Integral Curves and Flows” of Introduction to Smooth Manifolds by John Lee.

For any \(F \in \reals\), let \(\tau(F, x_0)\) denote the first time \(t \geq 0\) at which the positive gradient flow \(\eqref{posgradflow}\) leaves the sublevel set \[\{x \in \reals^d : f(x) < F\},\] with the convention that \(\tau(F, x_0) = +\infty\) if the flow never leaves the sublevel set in finite time. As a shorthand, we also define \[\tau(x) := \tau(0, x).\] Note that if \(\nabla f(x_0) \neq 0\) and \(\tau(F, x_0)\) is finite, then it is the only time \(t\) for which \(f(x(t)) = F\), since \(f(x(t))\) is increasing. For a given \(F\), we can define a map \(x \mapsto \tau(F, x)\) from \(\reals^d\) to \([0, \infty]\). We have the following useful fact.

Lemma 1

Let \(f \colon \reals^d \to \reals\) be \(C^\infty\), and let \(x_0 \in \reals^d, F \in \reals\). Assume \(\tau(F, x_0)\) is finite. Then the map \[x \mapsto \tau(F, x)\] is finite and differentiable in a neighborhood of \(x_0\).

Proof of Lemma 1

The main idea is to apply the implicit function theorem. At the end, we also sketch another approach based on rescaling/reparameterizing the gradient flow.

We know that \((x, t) = (x_0, \tau(F, x_0))\) is a solution of the equation \[f(\Phi(x, t)) = F\] recalling the definition \(\eqref{flowmap}\) of the flow map \(\Phi\). To apply the implicit function theorem, we need to check that the \(t\)-differential of \(f(\Phi(x, t))\) is nonzero at \((x, t) = (x_0, \tau(F, x_0))\). Indeed, \[\frac{d}{dt}[f(\Phi(x_0, t))]_{t = \tau(F, x_0)} = \D f(\Phi(x_0, \tau(F, x_0)))[x'(\tau(F, x_0))] = \|\nabla f(x(\tau(F, x_0)))\|^2,\] which is nonzero since gradient flow cannot reach a \(1\)-critical point in finite time.

Hence applying the implicit function theorem, there is a neighborhood \(U\) of \(x_0\) and a unique differentiable function \(T \colon U \to \reals\) such that \[f(\Phi(x, T(x))) = F, \quad \quad \forall x \in U.\] Due to the uniqueness of \(\tau\) mentioned previously, we conclude that \(\tau(F, x) = T(x)\), which proves the lemma.

---

For those curious, let’s sketch an alternative approach, employing a useful trick. Consider the rescaled positive gradient flow: \[x’(s) = \frac{\nabla f(x(s))}{\|\nabla f(x(s)\|^2}, \quad x(0) = x_0.\] Recall that multiplying the vector field of a flow by a positive function just amounts to reparameterizing time, so the flow lines of \(x(\cdot)\) do not change, just their time parameterization does.

This rescaled/reparameterized flow has the property that it crosses level sets at constant speed, as \[\frac{d}{ds}[f(x(s))] = 1.\] In particular, the time \(s\) at which the flow leaves the sublevel set \(\{x \in \reals^d : f(x) < F\}\) equals \(s = F - f(x_0)\), provided \(F \geq f(x_0)\) and we are careful to control where \(\nabla f\) vanishes. We can then conclude that \(x \mapsto \tau(F, x)\) is a differentiable function of \(s = F - f(x)\), which itself is smooth.

The Łojasiewicz inequality

In the 1960s, Stanisław Łojasiewicz proved the following theorem, which is an extremely useful tool for controlling gradient flows. (Notation: throughout, \(B(0, \delta)\) denotes the open ball of radius \(\delta\) centered at the origin.)

Theorem: Łojasiewicz Inequality

Let \(f \colon \reals^d \to \reals\) be real-analytic, with \(f(0) = 0\). There exist \(\delta_L > 0, c > 0, \mu \in [0, 1)\), such that \[ \begin{align}\label{Lojasiewiczinequality}\tag{Ł} \|\nabla f(x)\| \geq c |f(x)|^{\mu} \quad \quad \forall x \in B(0, \delta_L) =: U_L. \end{align} \]

Inequality \(\eqref{Lojasiewiczinequality}\) is known as the Łojasiewicz inequality — its proof is beyond the scope of this blog.

If \(f\) satisfies the Łojasiewicz inequality, then its gradient flows cannot stray too far from their starting points.

Lemma 2: Łojasiewicz inequality implies growth

Assume \(f\) is \(C^\infty\), has \(f(0) = 0, \nabla f(0) = 0\), and satisfies the Łojasiewicz inequality \(\eqref{Lojasiewiczinequality}\) with constants \(c, \mu\) in neighborhood \(U_L = B(0, \delta_L)\). There is a neighborhood \(U_M = B(0, \delta_M), \delta_M \leq \delta_L/2,\) such that if \(x(t)\) is the positive gradient flow \(\eqref{posgradflow}\) started from \(x_0 \in U_M\) with \(f(x_0) < 0\), then \[x(t) \in U_L \quad \quad \text{for all $t \in [0, \tau(x_0)]$}\] and moreover \[ \begin{align} \label{star1eqn} \tag{localization} \|x_0 - x(t)\| \leq (c(1-\mu))^{-1} |f(x_0)|^{1-\mu} \quad \quad \text{for all $t \in [0, \tau(x_0)]$}. \end{align} \]

In Lemma 2, \(\tau(x(0))\) may be either finite or infinite. If it is infinite, then \(x(t)\) must converge to a critical point of \(f\) (e.g., see the exercise at the end of this section), and \(x(\tau(x(0)))\) is that limiting point. Either way, \(x(\tau(x(0)))\) lies on the level set \(\{x : f(x) = 0\}\).

The proof of Lemma 2 is classical and originally due to Łojasiewicz. We present a proof based on Theorem 2.2 of this paper by Absil, Mahony and Andrews.

Proof of Lemma 2

Take any \(x(0) \in U_L\), and let \(T\) be the first time the positive gradient flow starting at \(x(0)\) leaves the set \(\{x \in U_L : f(x) < 0\}\). For \(t \in [0, T)\), we have \(f(x(t)) < 0\) and \[ \begin{align} \frac{d}{dt}\Big[ (- f (x(t)))^{1-\mu} \Big] &= (1-\mu) (- f(x(t)))^{-\mu} \frac{d}{dt}[- f(x(t))] \\ &= -(1-\mu) |f(x(t))|^{-\mu} \D f(x(t))[x'(t)] \\ &= -(1-\mu) |f(x(t))|^{-\mu} \|\nabla f(x(t))\| \cdot \|x'(t)\| \\ &\leq -c(1-\mu) |f(x(t))|^{-\mu} |f(x(t))|^{\mu} \cdot \|x'(t)\| \\ &= -c(1-\mu) \|x'(t)\|. \end{align} \] Therefore, for any \(t \in [0, T)\) we have \[ \begin{align}\label{usefulinequality}\tag{1} \|x(0) - x(t)\| &\leq \int_0^t \|x'(\tau)\| d \tau \leq (c(1-\mu))^{-1} \Big[|f(x(0))|^{1-\mu} - |f(x(t))|^{1-\mu}\Big] \\ &\leq (c(1-\mu))^{-1} |f(x(0))|^{1-\mu}. \end{align} \] The first inequality is because \(\int_0^t \|x'(\tau)\| d \tau\) is the length of the curve \(x(\cdot)\) between \(x(0)\) and \(x(t)\).

By smoothness of \(f\) and \(f(0) = 0\), there exists a \(\delta_M > 0\) such that \[ \begin{align}\label{deltaM}\tag{2} \|x\| + (c(1-\mu))^{-1} |f(x)|^{1-\mu} \leq \delta_L / 2, \quad \quad \forall x \in B(0, \delta_M). \end{align} \] We claim that any positive gradient flow started at \(x(0) \in U_M\) stays in \(B(0, \delta_L/2) \subseteq U_L\) until time \(t = \tau(x(0))\). For contradiction, assume not. Then for \(t\) close to \(T\), \(x(t)\) is arbitrarily close to the boundary of \(U_L\) (i.e., \(\|x(t)\|\) is close to \(\delta_L\)). On the other hand, inequalities \(\eqref{usefulinequality}\) and \(\eqref{deltaM}\) imply \[ \begin{align} \|x(t)\| \leq \|x(0)\| + (c(1-\mu))^{-1} |f(x(0))|^{1-\mu} \leq \delta_L/2 \quad \quad \forall t \in [0, T) \end{align} \] which is a contradiction, proving our claim.

We conclude that \(x(t) \in B(0, \delta_L/2)\) and equation \(\eqref{usefulinequality}\) holds if \(x(0) \in U_M\) and \(t \in [0, \tau(x(0)))\). We leave it as a (simple) exercise to verify this also holds for \(t \in [0, \tau(x(0))]\).

Exercise: Assume \(f\) satisfies the Łojasiewicz inequality \(\eqref{Lojasiewiczinequality}\) with constants \(c, \mu\) in \(U_L = B(0, \delta_L)\). Also assume that the gradient flow line \(x(\cdot)\) started at \(x(0) \in U_L\) stays in \(U_L\) for all \(t \geq 0\). Show that \(x(t)\) must converge to a critical point of \(f\). [Hint: Use Lemma 2, with a compactness argument.]

Proofs of Propositions 1 and 2: When does \(p\)-critical imply local minimum?

We are now ready to prove Proposition 4 below. Propositions 1 and 2 are immediate consequences.

Proposition 4

Suppose \(f \colon \reals^d \to \reals\) is \(C^\infty\) with \(f(0) = 0\), and satisfies the Łojasiewicz inequality \(\eqref{Lojasiewiczinequality}\) with constants \(c, \mu\) in neighborhood \(U_L\). If \(0\) is \(p\)-critical through neighborhoods for some \(p > (1-\mu)^{-1} - 1\), then \(0\) is a local minimum of \(f\).

Proof of Proposition 4

By definition of \(p\)-criticality through neighborhoods, there is a \(\delta_p > 0, C_p > 0\) such that \[ \begin{align}\label{pcriticality}\tag{$p$-criticality} f(x) - f(0) = f(x) \geq -C_p \|x\|^{p+1} \quad \quad \forall x \in B(0, \delta_p). \end{align} \] Suppose, for contradiction, that \(0\) is not a local minimum. Then by Proposition 3 there exists a \(x_0 \in U_L \cap B(0, \delta_p)\) such that positive gradient flow \(x(t)\) started from \(x(0) = x_0\) converges to \(0\) (and stays in \(U_L \cap B(0, \delta_p)\) and has \(f(x(t)) < 0\)). In particular, invoking Lemma 2, we have \[\|x(t)\| \leq (c(1-\mu))^{-1} |f(x(t))|^{1-\mu} \quad \quad \forall t \geq 0.\] On the other hand, \(\eqref{pcriticality}\) says \[|f(x(t)| \leq C_p \|x(t)\|^{p+1}.\] Putting these together, we have for all \(t \geq 0\): \[\|x(t)\| \leq (c(1-\mu))^{-1} C_p^{1-\mu} \|x(t)\|^{(p+1)(1-\mu)}.\] This is a contradiction since \((p+1)(1-\mu) > 1\) and \(\|x(t)\| \to 0\).

Proposition 1 follows immediately from Proposition 4 and Łojasiewicz’s theorem previously stated.

Proposition 2 follows immediately from Proposition 4, and bounds on the best Łojasiewicz exponent \(\mu\) given by D’Acunto and Kurdyka. Specifically, D’Acunto and Kurdyka show that if \(f \colon \reals^d \to \reals\) is a degree-\(k\) polynomial, then \(f\) satisfies the Łojasiewicz inequality with exponenent \(\mu = 1 - (3 k)^{-d}\).

Proof of Proposition 3: every saddle has a gradient flow line converging to it

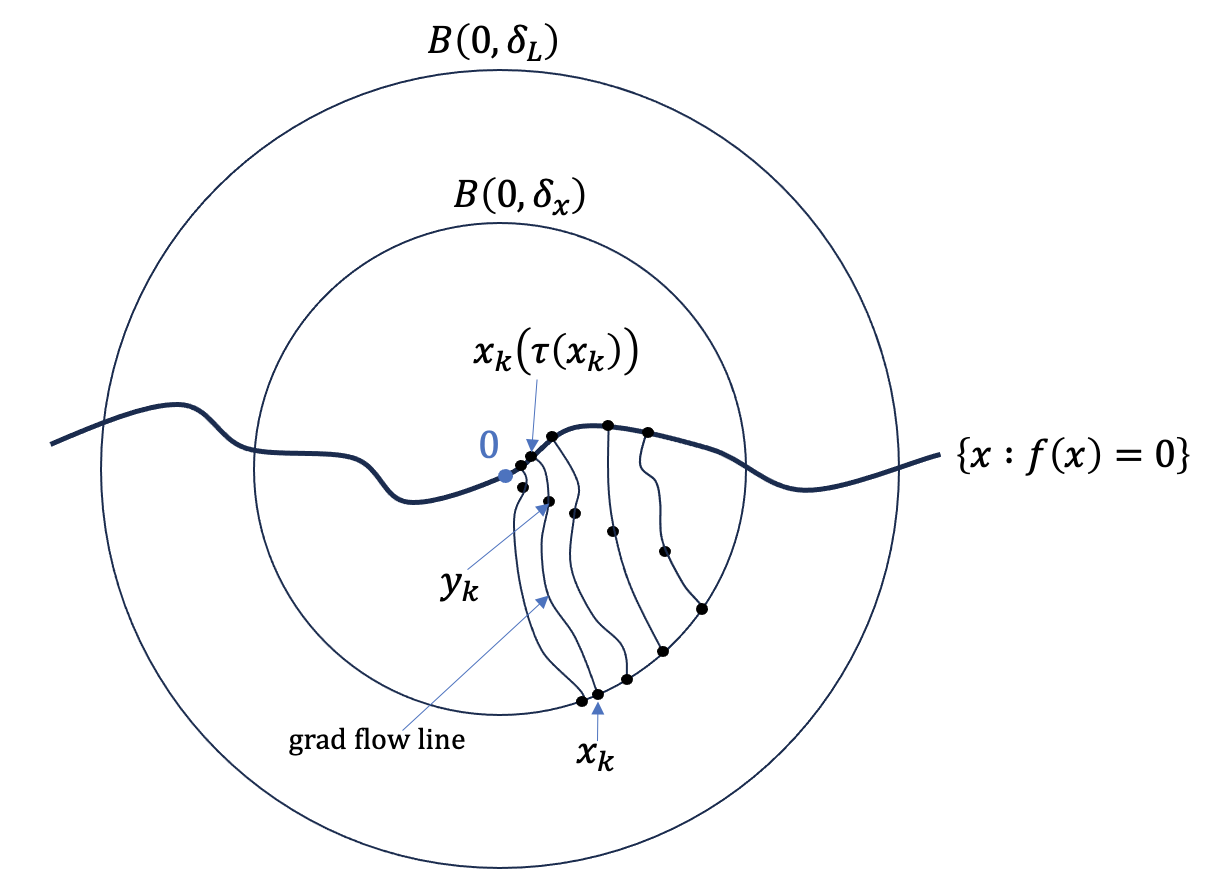
It remains to only prove Proposition 3. The idea is simple. Choose a sequence of points \(y_0, y_1, \ldots\) converging to \(0\) with \(f(y_k) < 0\). For each \(y_k\) we look at the positive gradient flow line \(y_k(\cdot)\) starting at \(y_k\) until it leaves the sublevel set \(\{x : f(x) < 0\}\). By Lemma 2, the endpoints \(y_k(\tau(y_k))\) of the flow lines also converge to 0.

Now run the negative gradient flow starting from \(y_k\) until it first hits the boundary of \(B(0, \delta_x), \delta_x > 0\); call the intersection point \(x_k\). Then we know that the positive gradient flow line starting at \(x_k\) ends at \(y_k(\tau(y_k))\), which converges to \(0\) as \(k \to \infty\).

The sequence \(x_0, x_1, \ldots\) accumulates to some \(x_\infty\) on the boundary of \(B(0, \delta_x)\). It stands to reason that the positive gradient flow line started from \(x_\infty\) converges to \(0\). This is indeed true. Let’s look at the details.

Figure 2: Diagram corresponding to proof of Proposition 3.

Proof of Proposition 3

We know that \(f\) satisfyies the Łojasiewicz inequality \(\eqref{Lojasiewiczinequality}\) with constants \(c, \mu\) in a neighborhood \(U_L = B(0, \delta_L)\). By Lemma 2, we know there is a neighborhood \(U_M = B(0, \delta_M), \delta_M \leq \delta_L/2,\) such that if \(x(0) \in U_M\) and \(f(x(0)) < 0\) then \(x(t) \in U_L\) for all \(t \in [0, \tau(x(0))]\).

Constructing the sequence \(\mathbf{y_0, y_1, \ldots \to 0}\): Since \(0\) is not a local minimum, there is a sequence of points \(y_0, y_1, \ldots\) in \(U_M\) which converges to \(0\), and satisfies \(f(y_k) < 0\) for all \(k\). Let \(y_k(t)\) denote positive gradient flow started at \(y_k(0) = y_k\). Equation \(\eqref{star1eqn}\) of Lemma 2, tells us that the entire trajectories \(\{y_k(t) : t \in [0, \tau(y_k)]\}\) converge to \(0\), since \(y_k \to 0\) and \(f(y_k) \to 0\). In particular, we conclude \(f(y_k(\tau(y_k))) = 0\), and \(y_k(\tau(y_k))\) converges to \(0\) as \(k \to \infty\).

Constructing the sequence \(\mathbf{x_0, x_1, \ldots \to x_\infty}\): Consider the negative gradient flow lines started from each \(y_k\). Observe that each of these flows must eventually leave the ball \(U_L\) (otherwise they are trapped and must converge to a critical point, which must have function value 0 by the Łojasiewicz inequality, a contradiction). Fix \(\delta_x \in (\delta_M, \delta_L)\). For each \(k\), let \(x_k\) be the first point where this negative gradient flow crosses the boundary of \(B(0, \delta_x)\) (so \(\|x_k\| = \delta_x\)).

Let \(x_k(t)\) denote the positive gradient flow starting from \(x_k(0) = x_k\). Without loss of generality (by compactness and taking a convergent subsequence), we can assume \(x_0, x_1, x_2, \ldots\) converge to some \(x_\infty\) (of course with \(\|x_\infty\| = \delta_x\)). Let’s summarize what we know about the positive gradient flows \(x_k(t)\):

1. Each flow starts at \(x_k(0) = x_k\) on the boundary of \(B(0, \delta_x)\), and \(f(x_k) < 0\).

2. \(x_k(t) \in U_L\) for all \(k \geq 0\) and \(t \in [0, \tau(x(0))]\).

3. \(x_k(\tau(x_k)) = y_k(\tau(y_k))\) converges to \(0\), and \(f(x_k(\tau(x_k))) = 0\) for all \(k \geq 0\).

Finishing up: To conclude, we want to show that \(x_\infty(t)\), the positive gradient flow starting from \(x_\infty\), converges to \(0\) as \(t \to \tau(x_\infty)\). That is, we want to show that for each \(\epsilon > 0\), there is a \(T \in (0,\tau(x_\infty))\) such that \(\|x_\infty(t)\| \leq \epsilon\) for all \(t \in [T, \tau(x_\infty))\).

So let \(\epsilon \in (0, \delta_x)\). Choose \(K\) big enough so that \(\|x_k(\tau(x_k))\| \leq \epsilon / 4\) for all \(k \geq K\) (which we can do by property iii). Equation \(\eqref{star1eqn}\) of Lemma 2 gives us \[\delta_x / 2 < \delta_x - \epsilon/4 \leq \|x_k - x_k(\tau(x_k))\| \leq (c(1-\mu))^{-1}|f(x_k)|^{1-\mu}\] for all \(k \geq K\). In other words, this gives us a lower bound on \(|f(x_k)|\) in terms of \(\delta_x\).

Define \(F_\epsilon < 0\) through \[(c(1-\mu))^{-1} |F_\epsilon|^{1-\mu} = \epsilon / 4.\] From this and \(\epsilon / 4 < \delta_x / 2\), we find that \(|F_\epsilon| < |f(x_k)|\) for all \(k \geq K\), and so \(0 < \tau(F_\epsilon, x_k) < \tau(x_k)\) for \(k \geq K\). Additionally, equation \(\eqref{star1eqn}\) implies \[ \begin{align}\label{star2eqn}\tag{3} \|x_k(\tau(F_\epsilon, x_k))\| \leq \|x_k(\tau(x_k))\| + (c(1-\mu))^{-1} |F_\epsilon|^{1-\mu} \leq \epsilon/4 + \epsilon/4 = \epsilon/2 \quad \quad \forall k \geq K. \end{align} \]

By continuity of the flow map \(\Phi\) and continuity of \(x \mapsto \tau(F_\epsilon, x)\) (by Lemma 1), we have \[ \lim_{k \to \infty} \Phi(x_k, \tau(F_\epsilon, x_k)) = \Phi(x_\infty, \tau(F_\epsilon, x_\infty)) = x_{\infty}(\tau(F_\epsilon, x_\infty)), \] and \(\|x_{\infty}(\tau(F_\epsilon, x_\infty))\| \leq \epsilon/2\) by \(\eqref{star2eqn}\). Invoking equation \(\eqref{star1eqn}\) one more time, we conclude \[\|x_{\infty}(t)\| \leq \|x_{\infty}(\tau(F_\epsilon, x_\infty))\| + (c(1-\mu))^{-1} |F_\epsilon|^{1-\mu} \leq \epsilon / 2 + \epsilon / 4 \leq \epsilon\] for all \(t \in [\tau(F_\epsilon, x_\infty), \tau(x_\infty))\), as desired.

---

Acknowledgements: We thank Nicolas Boumal for several helpful pointers.